摘要
文章在重新思考现有人工神经网络的非线性表示能力和新皮层列的功能的基础上,提出了一种基于记忆的神经网络理论,它由两种新的人工神经网络模型:nmODE和-net和两种学习算法:NMLA和-LA组成。(笔记只探究了nmODE和nmLA)
nmODE是一种将学习神经元和记忆神经元分离开来的特殊结构。给定任何外部输入,nmODE具有全局吸引子特性,因此嵌入了内存机制。nmODE建立了从外部输入到其相关吸引子的非线性映射,并且不存在与输入数据空间同胚的学习特征问题。
术语与问题表述
一般的神经ODE可以描述为
对于,其中表示网络的状态,表示外部输入变量,并将其作为数据输入,函数是连续的,满足条件,从而保证解的存在唯一性
向量被称为神经ODE的平衡点,如果它满足
全局吸引子必须是平衡点,另外,它吸引了所有的轨迹。
假设neuralODE具有全局吸引子性质,则neuralODE建立了从输入x到相关吸引子的定义良好的非线性映射。

将数据输入到神经ODEs有两种方法。一种方法是保持外部输入x固定,并使用初始y(0)作为网络输入;另一种方法是保持初始y(0)固定,并使用外部输入x作为网络输入。大多数现有的neuralODEs采用第一种方法。在文章中,使用了第二种方法进行数据输入。当使用初始的y(0)作为数据输入时,神经ODEs在保持输入数据空间拓扑结构的学习表示方面有很大的缺点。
神经记忆常微分方程(nmODE)
单层网络
是矩阵,是维的输入向量,是维的偏置向量,是维的输出向量。激活函数f传统上是一个不减函数,如函数、函数或函数等
单层网络由于其非线性程度不够高,无法解决XOR分类问题
一个简单的增加单层网络非线性的方法是消除激活函数不减的约束。一个例子是使用sin2(⋅)函数作为激活函数,即
隐映射方程
另一种增加单层网络非线性的方法是使用隐式函数.通过对网络表示进行简单的修改,我们可以得到如下形式的隐式映射方程:
这个隐式映射方程的非线性程度明显高于,将从输入到输出的非线性映射定义为:
结合上述增加非线性的方法,提出一个特定的隐式映射方程
或等效于组件形式
神经记忆常微分方程
隐式映射方程可以看作是常微分方程的平衡方程。为了求解这一平衡方程,本文提出了一个名为nmODE的神经记忆常微分方程:
或组件形式
对于 代表网络的外部输入,表示网络在时间处的状态,是初始值。用于表示外部输入变量的每个神经元称为输入神经元,而用于表示状态的任何神经元都称为记忆神经元。
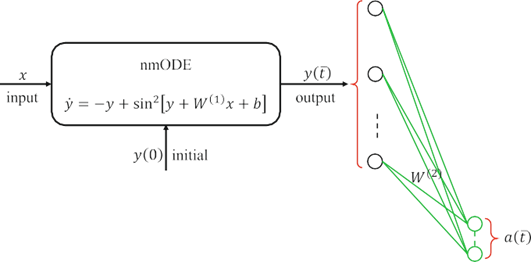
- 性质
- nmODE可以简单地通过求解方程中每个i的一维ODE来求解,因为这些一维ODE是相互独立的
- 每个学习连接只从一个输入神经元连接到记忆神经元,并且在任何记忆神经元之间没有学习连接,因此学习与记忆分离。这种结构使得该模型特别容易进行网络学习
- nmODE有且仅有一个全局吸引子,对于每个外部输入都具有全局吸引子性质,将吸引子看作内存存储机制可以嵌入到网络中
- nmODE可以是作为新皮层列的数学模型(理论神经科学的研究表明,新皮层中的每一列都可能扮演着情报单位,列必须具有完整的内存机制)
nmLA

生物学观点
最近提出了另一个令人惊讶的想法,即大脑中的智力单元是皮层柱,每个脑柱都可以利用赋予的参考框架属性来学习建模世界。由于列运行一个通用算法,为了完成任务,需要多个列一起进行决策。霍金斯认为,这一进程是通过投票实现的。他把这个理论称为“一千个大脑”。
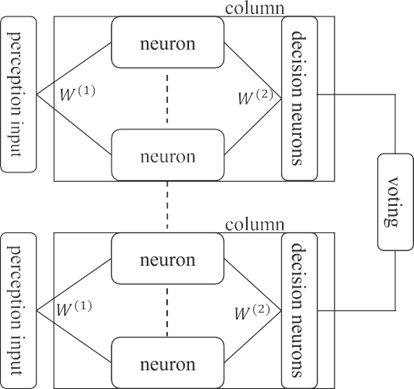
-net
-net是由迭代方程描述的nmode的一个离散版本
实验
MNIST
- 全局吸引子可视化
 同一类的吸引子非常相似,而属于不同类别的吸引子则明显不同。这些结果表明,所提出的nmODE有效地捕捉了MNIST数据集中10个类的本质特征
同一类的吸引子非常相似,而属于不同类别的吸引子则明显不同。这些结果表明,所提出的nmODE有效地捕捉了MNIST数据集中10个类的本质特征
- t-SNE可视乎
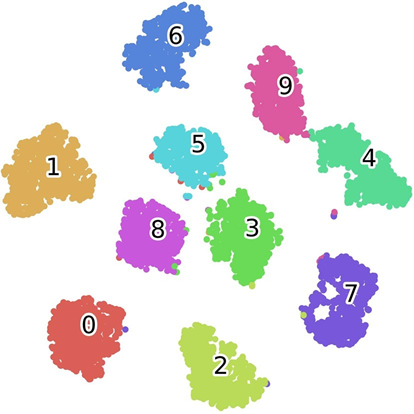




 同一类的吸引子非常相似,而属于不同类别的吸引子则明显不同。这些结果表明,所提出的nmODE有效地捕捉了MNIST数据集中10个类的本质特征
同一类的吸引子非常相似,而属于不同类别的吸引子则明显不同。这些结果表明,所提出的nmODE有效地捕捉了MNIST数据集中10个类的本质特征