Diffusion数学推导
生成模型
基于
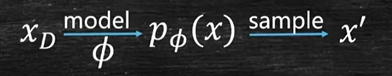
VAE
Variational AutoEncoder
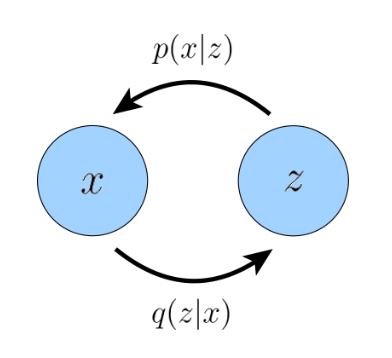
Encoder:
Decoder:
对于潜在变量(latent variable) z 的分布
优化目标
目标:使得建模的
但是直接建模
是非常困难的。
(1)边缘化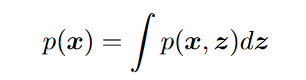
(2)链式法则
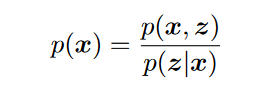
引出ELBO
表达式如下: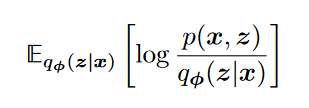
其中,
是一个近似变分分布,其参数为我们寻求优化的 同时和
满足关系 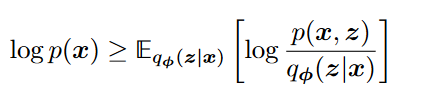
- 证明:
(1)琴声不等式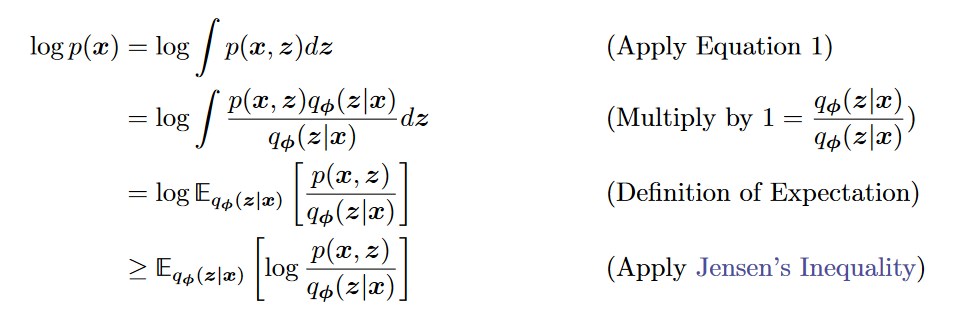 (2) KL散度
(2) KL散度 
- 证明:
优化目标的转变
优化VAE,其实就是最大化ELBO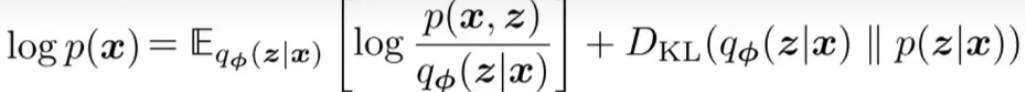
解释:VAE是通过decoder和encoder分别拟合
和 ,来间接拟合 。
上式KL散度反映的就是encoder对真实的拟合程度,要最小化它。但是直接优化KL散度不现实,因为不知道 这个 。
是真实的数据分布,对于给定数据集,是一个固定的值,与模型无关。
所以最小化KL散度等价于最大化ELBOELBO的解释

- 最大化
: 让 能最大可能的从隐变量 生成原始数据x。 - 最小化
:让 将真实数据 映射到隐变量 后, 尽量能满足我们指定的分布,一般为 : 如果把 这项损失去掉,就是AE模型。没有P项, 没有趋向于正态分布,故AE的 分布未知,没法有效采样,所以也不能作为生成模型。
- 最大化
VAE架构
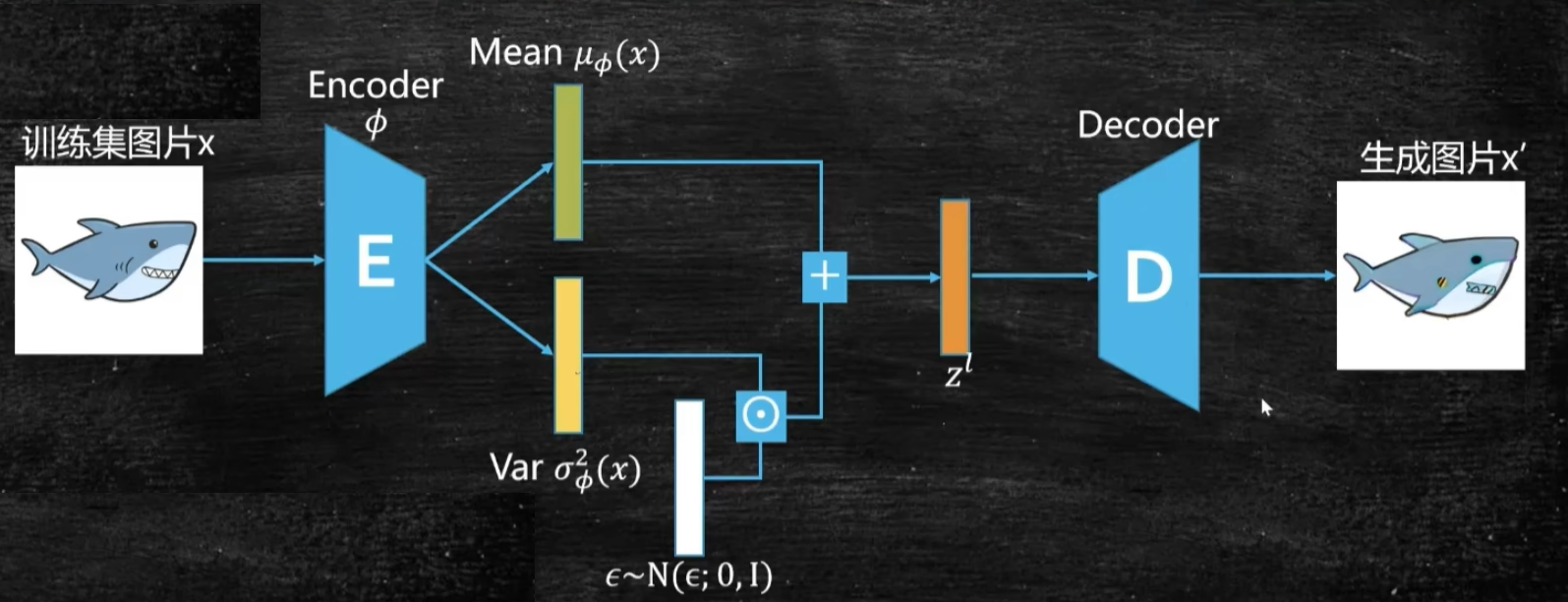
图中公式:
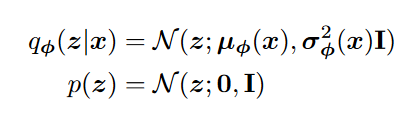
优化目标的均值项使用蒙特卡洛模拟采样
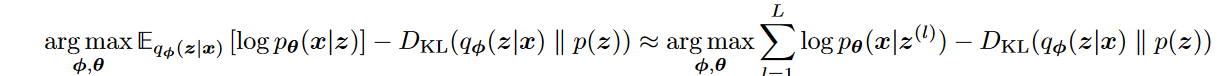
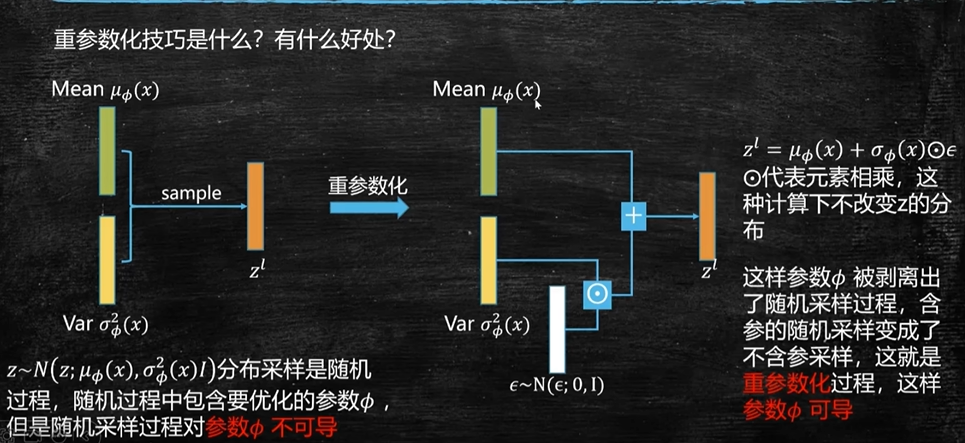
重参数化
MHVAE
Markovian Hierarchical Variational AutoEncoder
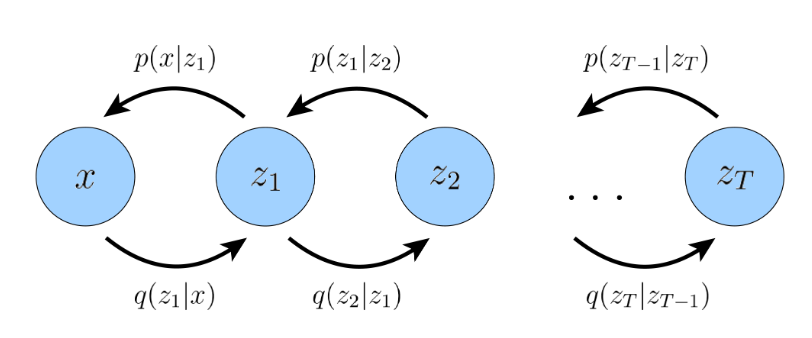
MHVAE 就是级联的马尔可夫VAE链
和 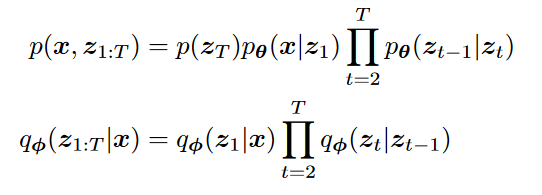
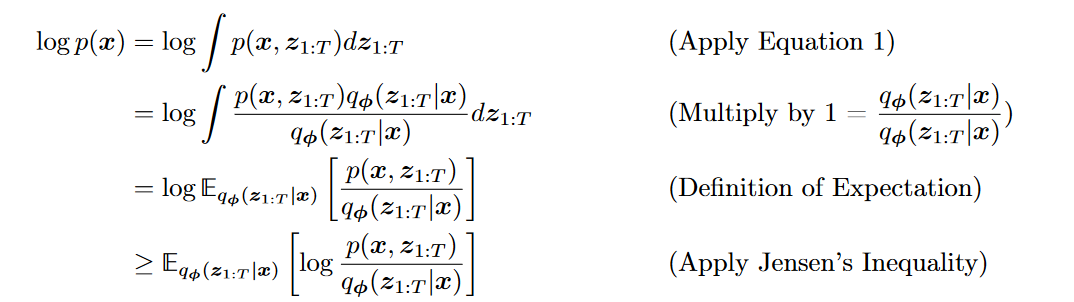
VDM
Variational Diffusion Model
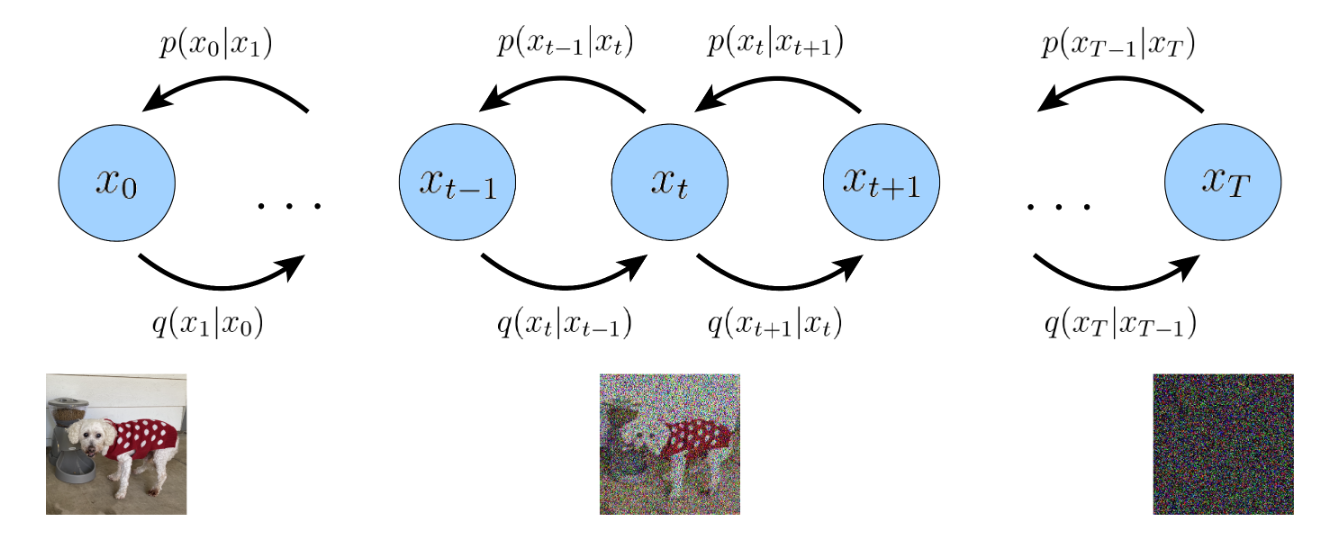
从MHVAE到VDM
- 三个限制
- 数据x和所有隐变量z的维度相同
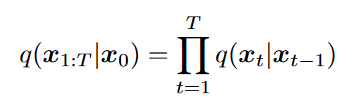
- 每个时间步的潜在编码器的结构都没有被学习;它被预先定义为线性高斯模型。换句话说,它是一个以前一个时间步的输出为中心的高斯分布
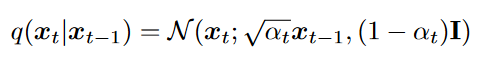 其中
其中 - 最终时间步长 T 的潜在分布是标准高斯分布
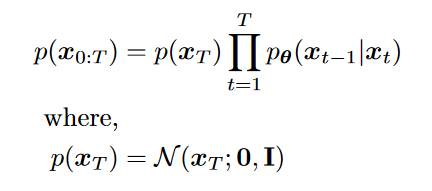
- 数据x和所有隐变量z的维度相同
ELBO的解释
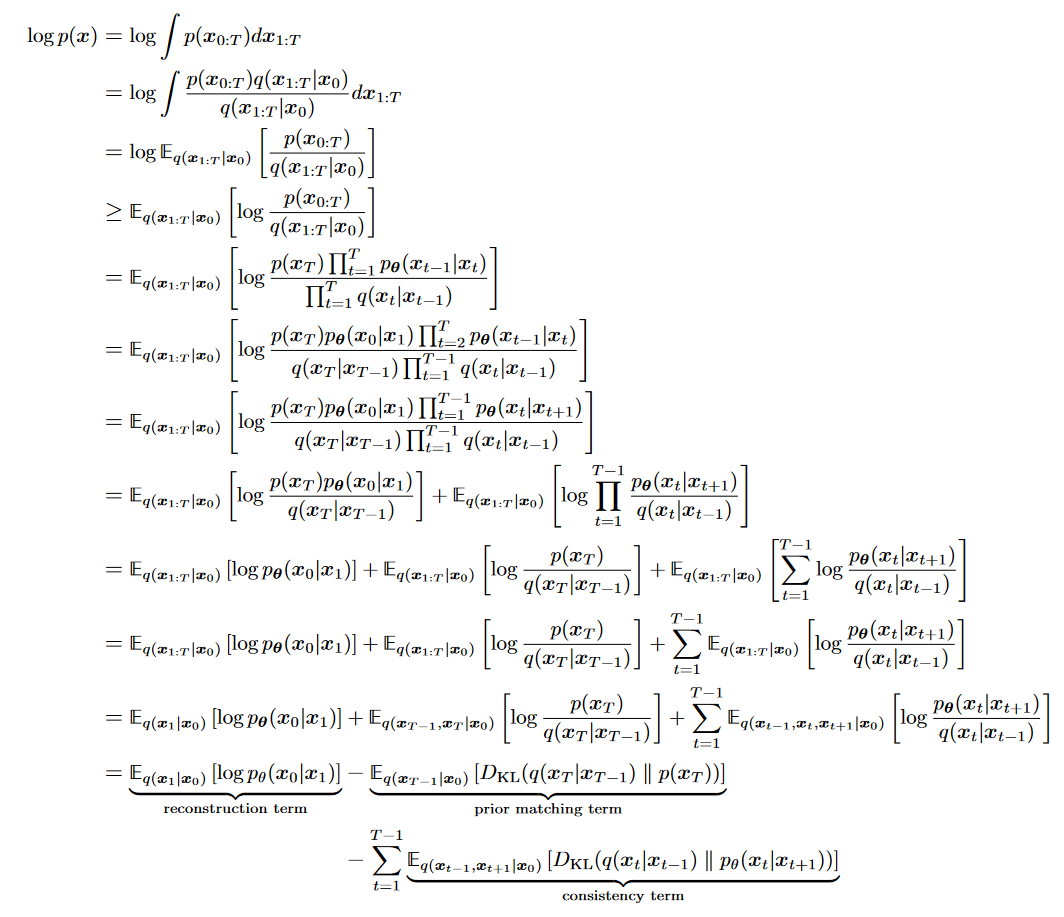
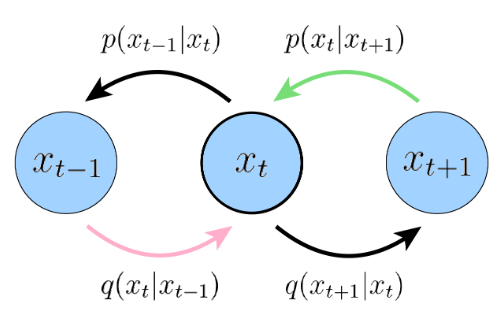
粉色和绿色箭头指的Consisitency term的KL散度
- Prior matching term最后一步推导

- Consisitency term最后一步推导

问题与改进
最后的Consisitency中需要对两个变量进行蒙特卡洛模拟,可能有较大的方差。
采用贝叶斯定理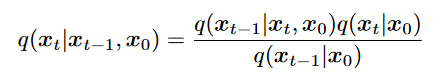
重写ELDBO


如何求出去噪项的
答:使用贝叶斯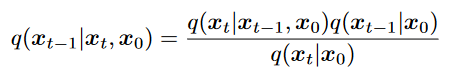
递推
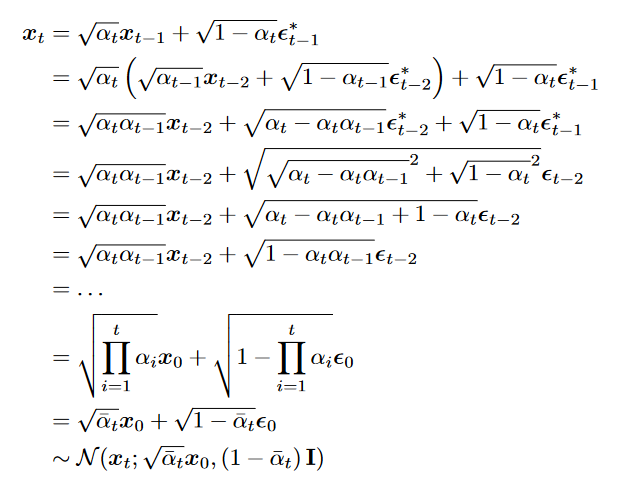
代入

特性
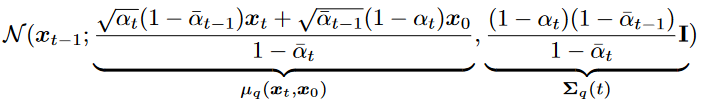
- 是个高斯分布
- 方差
只和 有关,故是个常数 - 均值
是关于 的函数
Loss
拟合均值
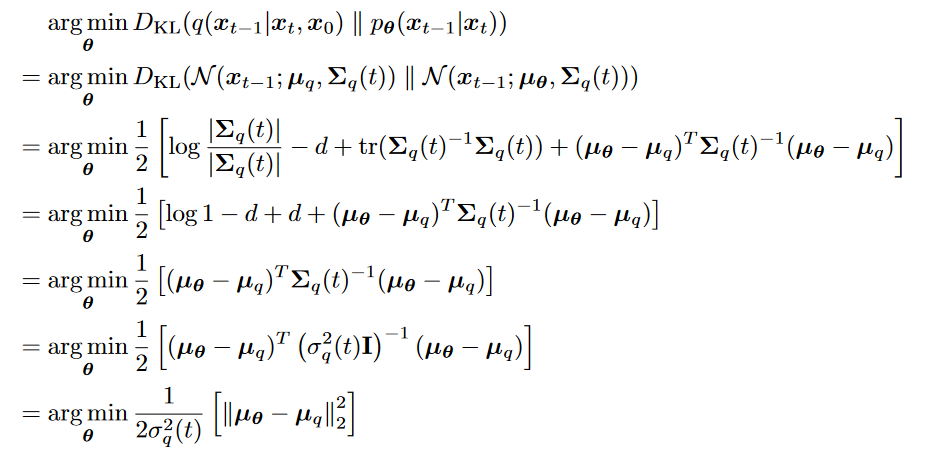
其中两个高斯分布的KL散度为
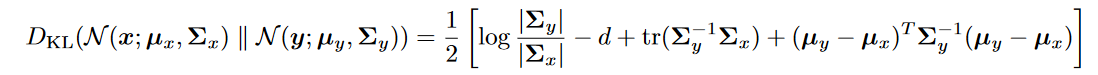
最小化KL散度等价于拟合
的均值 拟合
均值的表达式
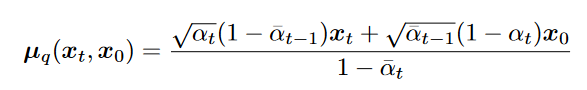
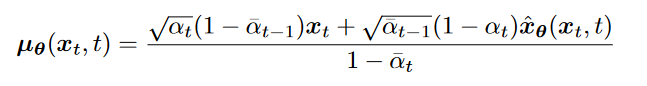
拟合
的推导 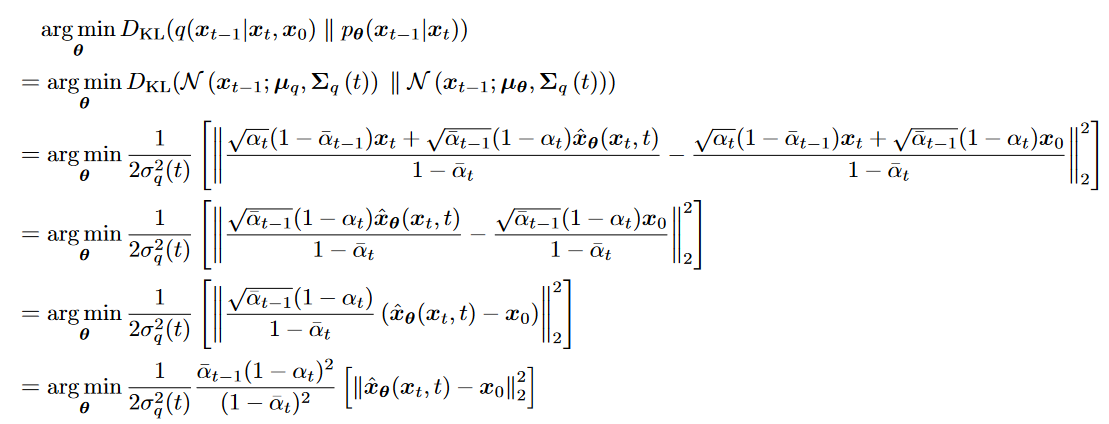
最小化KL散度等价于根据
和 拟合 拟合噪声
用噪声表达
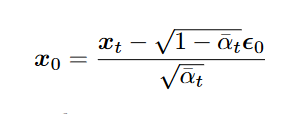
待入
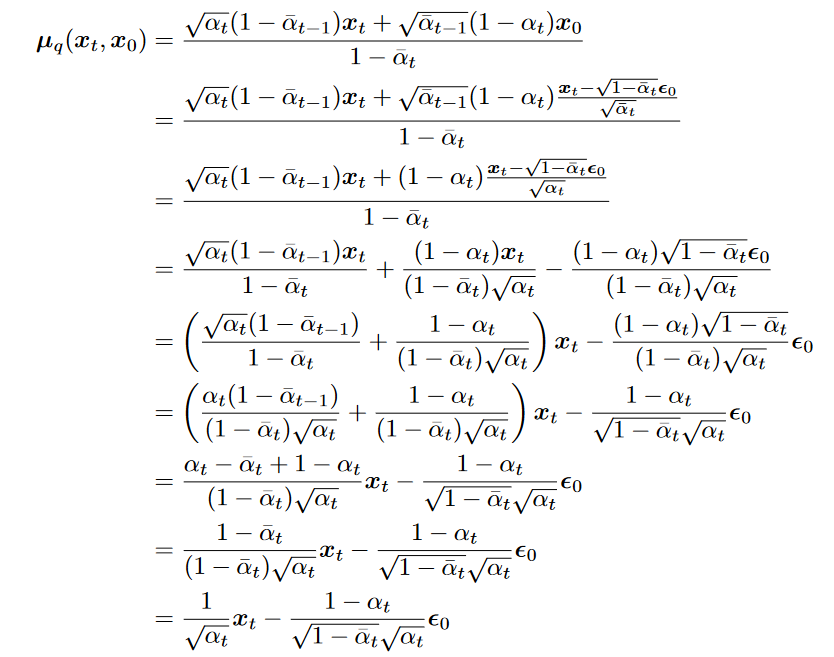
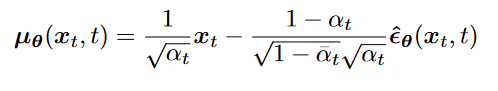
拟合噪声的推导
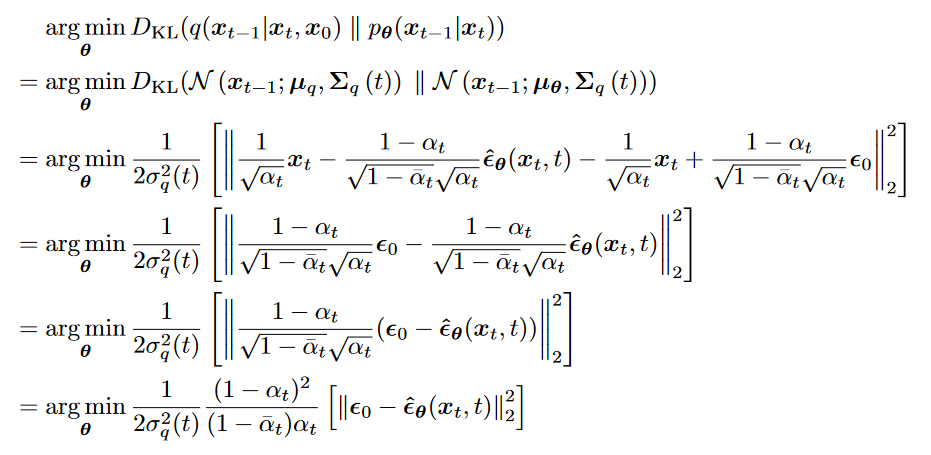
Inference
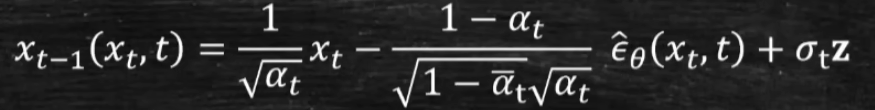
- 标题: Diffusion数学推导
- 作者: M13c
- 创建于 : 2024-09-26 15:57:25
- 更新于 : 2024-09-26 22:40:35
- 链接: https://m13c.top/Diffusion/Diffusion数学推导.html
- 版权声明: 版权所有 © M13c,禁止转载。