最优化理论

凸集

仿射集和凸集

• 仿射：

  1. 仿射集合

     如果集合C中两个不同的点的直线仍在集合C中, 则称集合C是仿射的

     等价于: 对满足

  2. 仿射组合（点）

     假设如果是一个仿射集合，并且，那么点仍在中

  3. 仿射包（集合）

• 凸集

  1. 凸集

     如果集合C中两个不同的点间的线段仍在集合C中, 则称集合C是凸集

     等价于: 对且满足

  2. 凸组合

     ，其中

  3. 凸包

• 锥

  1. 凸锥

     对且满足

  2. 锥组合

     ，其中

  3. 锥包

• 示例

  1. 超平面（）

  2. 半空间（）

  3. 球（）

  4. 椭球（）

保凸运算

• 交集: 凸集的交集仍为凸集

  如果对于任意的都是凸的, 那么所有的集合的交集也是凸的

• 仿射函数 (线性映射)

  • 定义

    如果是一个线性函数和一个常数的和, 即具有 的形式,, 函数

  • 结论1:

    假设S是凸的, 则S在f的映射下的象 也是凸的

    类似地, S在f下的原象 也是凸的

  • eg:

    伸缩

    平移

    和

    直积

• 透视函数

  • 定义

    为透视函数,

    1）通过透视函数，从降维到维

    2）最后一个元素，即t值，必须是正数

  • 结论

    如果为内的凸集，那么它的象也是凸的

    一个凸集在透视函数下的原象也是凸的

其他

• 超平面分离定理

  假设 和是两个不相交的凸集, 那么

  若没有等号，则成为严格分离

• 支撑超平面

  假设为集合边界上一点，如果并且对于有那么称超平面 为集合在处的超平面

凸函数

基本定理和例子

• 定义

  是非空凸集，定义在C上的函数，如果对满足
  
  

  
  
  则称为上的凸函数

  • 凹函数

    如果为凸函数，则为凹函数

  • 结论

    所有的仿射函数（线性函数）是既凸又凹的 反之若某个函数既凸又凹，则其为仿射函数

• 性质

• 一阶条件

• 二阶条件

• 例子

  • 二次函数

    

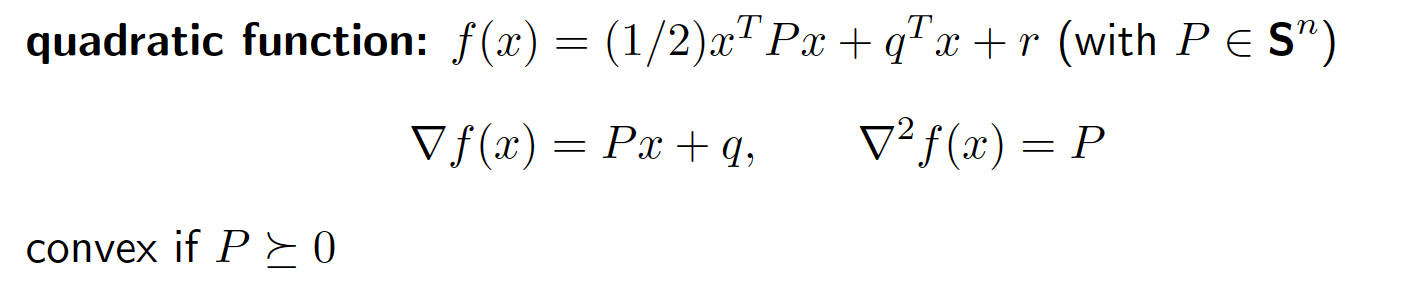
  • 常见函数

    

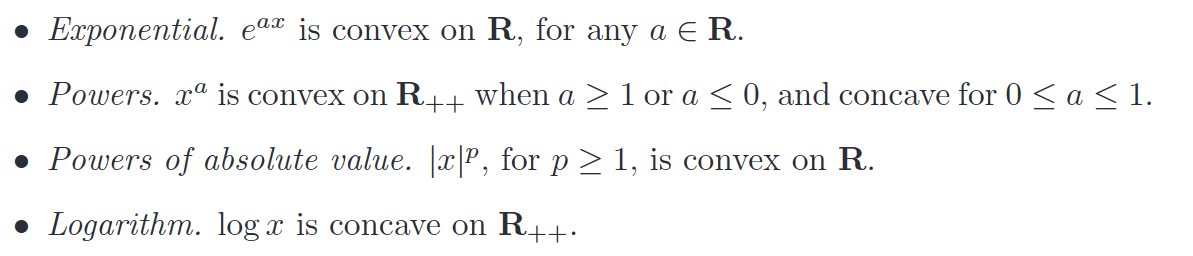
  • 有趣的函数

    

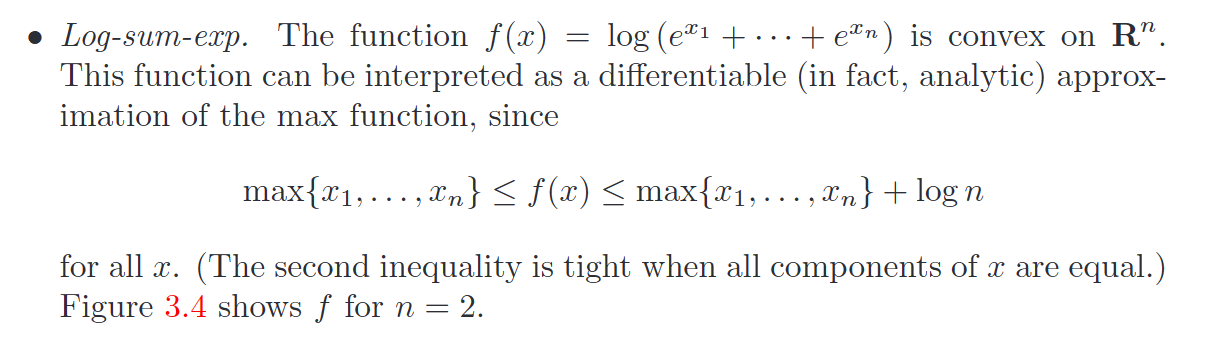
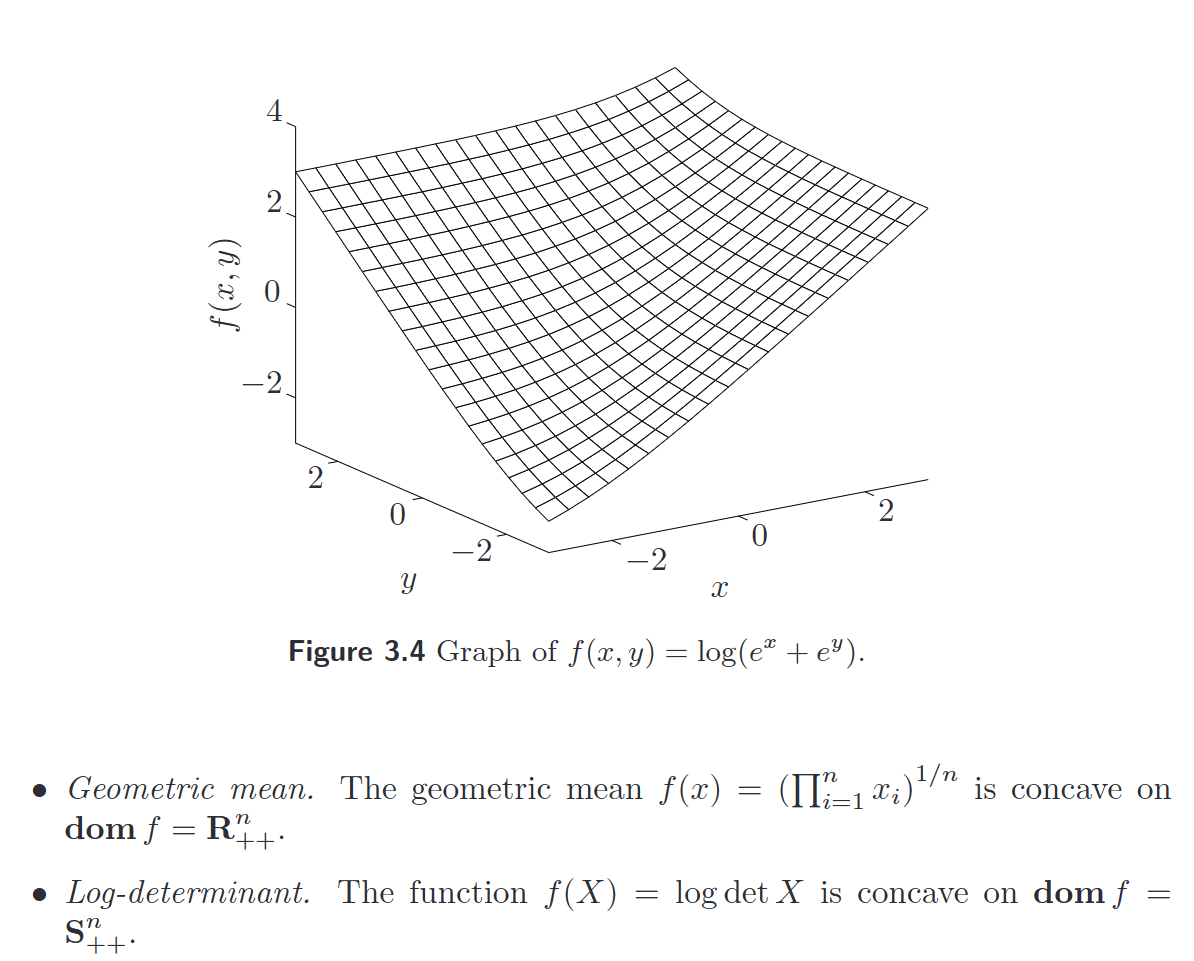
保凸运算

• 非负加权求和

• 复合仿射映射

• 逐点最大值

• 函数复合